Обладающих некоторым свойством.
В общем случае, геометрическое место точек формулируется предикатом , аргументом которого является точка данного линейного пространства. Параметры предиката могут носить различный тип. Предикат называется детерминантом геометрического места точек. Параметры предиката называются дифференциалами геометрического места точек (не путать с дифференциалом в анализе).
Роль дифференциалов во введении видовых различий в фигуру. Количество дифференциалов может быть любым; дифференциалов может и вовсе не быть.
Если заданы детерминант , где M {\displaystyle M} - точка, - дифференциалы, то искомую фигуру A {\displaystyle A} задают в виде: « A {\displaystyle A} - геометрическое место точек M {\displaystyle M} , таких, что P (M , a , b , c , …) {\displaystyle P(M,\;a,\;b,\;c,\;\ldots)} ». Далее обычно указывается роль дифференциалов, им даются названия применительно к данной конкретной фигуре. Под собственно фигурой понимают совокупность (множество) точек M {\displaystyle M} , для которых для каждого конкретного набора значений a , b , c , … {\displaystyle a,\;b,\;c,\;\ldots } высказывание P (M , a , b , c , …) {\displaystyle P(M,\;a,\;b,\;c,\;\ldots)} обращается в тождество. Каждый конкретный набор значений дифференциалов определяет отдельную фигуру, каждую из которых и всех их в совокупности именуют названием фигуры, которая задаётся через ГМТ.
В словесной формулировке предикативное высказывание озвучивают литературно, то есть с привлечением различного рода оборотов и т. д. с целью благозвучия. Иногда, в случае простых детерминантов, вообще обходятся без буквенных обозначений.
Пример : параболу зададим как множество всех таких точек M {\displaystyle M} , что расстояние от M {\displaystyle M} до точки F {\displaystyle F} равно расстоянию от M {\displaystyle M} до прямой l {\displaystyle l} . Тогда дифференциалы параболы - F {\displaystyle F} и l {\displaystyle l} ; детерминант - предикат P (M , F , l) = (ρ (M , F) = ρ l (M , l)) {\displaystyle P(M,\;F,\;l)=(\rho (M,\;F)=\rho _{l}(M,\;l))} , где ρ {\displaystyle \rho } - расстояние между двумя точками (метрика), ρ l {\displaystyle \rho _{l}} - расстояние от точки до прямой. И говорят: «Парабола - геометрическое место точек M {\displaystyle M} , равноудалённых от точки F {\displaystyle F} и прямой l {\displaystyle l} . Точку F {\displaystyle F} называют фокусом параболы, а прямую l {\displaystyle l} - директрисой».
Геометрическим местом точек называют множество точек , заданное условием, являющимся и свойством, и признаком .
Другими словами, все точки из рассматриваемого геометрического места точек, и только они , удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
| Дано | Найти | Ответ (ГМТ ) | Рисунок |
| Точка и число r | Геометрическое место точек , находящихся на расстоянии r от данной точки. | Окружность радиуса r | |
| Угол | Геометрическое место точек , равноудалённых от сторон данного угла. | Биссектриса угла |  |
| Пара пересекающихся прямых | Геометрическое место точек , равноудалённых от пары данных пересекающихся прямых. | Две перпендикулярных прямых (биссектрисы углов, образованных данными прямыми) |  |
| Отрезок | Геометрическое место точек , равноудалённых от концов данного отрезка. | Серединный перпендикуляр к отрезку |  |
| Прямая и число d | Геометрическое место точек , находящихся на расстоянии d от данной прямой. | Пара параллельных прямых |  |
| Пара параллельных прямых | Геометрическое место точек , каждая из которых равноудалена от двух данных параллельных прямых . | Прямая |  |
| Отрезок и угол , величина которого равна α | Геометрическое место точек , из которых данный отрезок виден под данным углом | Две дуги окружностей одинакового радиуса , для которых данный отрезок является общей хордой, причём из дуг исключены концы отрезка . |  |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике .
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
Геометрическим местом точек (в дальнейшем ГМТ), называется фигура плоскости, состоящая из точек обладающих некоторым свойством, и не содержащая ни одной точки, не обладающей этим свойством.
Мы будем рассматривать только те ГМТ, которые можно построить с помощью циркуля и линейки.
Рассмотрим ГМТ на плоскости, обладающие простейшими и наиболее часто выражающимися свойствами:
1) ГМТ, отстоящих на данном расстоянии r от данной точки О, есть окружность с центром в точке О радиуса r.
2) ГМТ равноудаленных от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ и проходящая через его середину.
3) ГМТ равноудаленных от двух данных пересекающихся прямых, есть пара взаимно перпендикулярных прямых, проходящих через точку пересечения и делящих углы между данными прямыми пополам.
4) ГМТ, отстоящих на одинаковом расстоянии h от прямой, есть две прямые, параллельные этой прямой и находящиеся по разные стороны от нее на данном расстоянии h.
5) Геометрическое место центров окружностей, касающихся данной прямой m в данной на ней точке М, есть перпендикуляр к АВ в точке М (кроме точки М).
6) Геометрическое место центров окружностей, касающихся данной окружности в данной на ней очке М, есть прямая, проходящая через точку М и центр данной окружности (кроме точек М и О).
7) ГМТ, из которых данный отрезок виден под данным углом, составляет две дуги окружностей, описанных на данном отрезке и вмещающих данный угол.
8) ГМТ, расстояния от которых до двух данных точек А и В находятся в отношении m: n, есть окружность (называемая окружностью Аполлония).
9) Геометрическое место середин хорд, проведенных из одной точки окружности, есть окружность, построенная на отрезке, соединяющем данную точку с центром данной окружности, как на диаметре.
10) Геометрическое место вершин треугольников равновеликих данному и имеющих общее основание, составляет две прямые, параллельные основанию и проходящие через вершину данного треугольника и ему симметричного относительно прямой, содержащей основание.
Приведем примеры отыскания ГМТ.
ПРИМЕР 2. Найти ГМТ, являющихся серединами хорд, проведенных из одной точки данной окружности (ГМТ № 9).
Решение . Пусть дана окружность с центром О и на этой окружности выбрана точка А из которой проводятся хорды. Покажем, что искомое ГМТ есть окружность, построенная на АО как на диаметре (кроме точки А) (рис. 3).
Пусть АВ - некоторая хорда и М - ее середина. Соединим М и О. Тогда МО ^ АВ (радиус, делящий хорду пополам, перпендикулярен этой хорде). Но, тогда ÐАМО = 90 0 . Значит М принадлежит окружности с диаметром АО (ГМТ № 7). Т.к. эта окружность проходит через точку О, то О принадлежит нашему ГМТ.
Обратно, пусть М принадлежит нашему ГМТ. Тогда, проведя через М хорду АВ и соединив М и О, получим, что ÐАМО = 90 0 , т.е. МО ^ АВ, а, значит, М - середина хорды АВ. Если же М совпадает с О, то О - середина АС.
Часто метод координат позволяет находить ГМТ.
ПРИМЕР 3. Найти ГМТ, расстояние от которых до двух данных точек А и В находятся в данном отношении m: n (m ≠ n).

Решение
. Выберем прямоугольную систему координат так, чтобы точки А и В располагались на оси Ох симметрично относительно начала координат, а ось Оу проходила через середину АВ (рис.4). Положим АВ = 2a. Тогда точка А имеет координаты А (a, 0), точка В - координаты В (-a, 0). Пусть С принадлежит нашему ГМТ, координаты С(х, у) и CB/CA = m/n.
Но ![]()
![]() Значит
Значит
 (*)
(*)
Преобразуем наше равенство. Имеем

Геометрическое место точек. Срединный перпендикуляр . Биссектриса угла.
Окружность. Круг. Центр окружности. Радиус. Дуга. Секущая. Хорда.
Диаметр. Касательная и её свойства. Сегмент. Сектор. Углы в круге.
Длина дуги. Радиан. Соотношения между элементами круга.
Геометрическое местоточек – этомножество всех точек,удовлетворя ющихопределённым заданным условиям.
П р и м е р 1. Срединный перпендикуляр любого отрезка есть геометрическое
место точек (т.е. множество всех точек), равноудалён ных от
концов этого отрезка. Пусть PO AB и AO = OB:
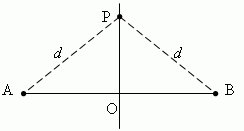
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d .
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
П р и м е р 2. Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон .
П р и м е р 3. Окружность есть геометрическое место точек (т.е. множе ство
всех точек), равноудалённых от её центра (на рис. пока зана одна
из этих точек – А).

Окружность - это геометрическое место точек (т.е. множество всех точек) на плоскости , равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R . Часть плоскости, ограниченная окружностью, называется кругом . Часть окружности (
Am B , рис.39 ) называется дугой. Прямая PQ , проходящая через точки M и N окружности ( рис.39 ), называется секущей, а её отрезок MN , лежащий внутри окружности - хордой.
Хорда, проходящая через центр круга (например,
BC, рис.39), называется диаметром и обозначается d или D . Диаметр – это наибольшая хорда, равная двум радиусам (d = 2 r ).
Касательная. Предположим, секущая PQ (рис.40) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K. Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K. По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K. Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
Свойства касательной.
1) К асательная к окружности перпендикулярна к радиусу, проведенному в точку касания ( AB OK, рис.40) .
2) Из точки, лежащей вне круга, можно провести две касательные к
одной и той же окружности; их отрезки равны (рис.41).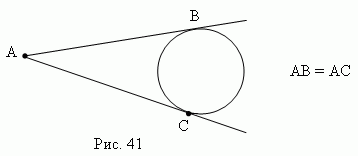
Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB (рис.42). Длина перпендикуляра CD, проведенного из середины хорды AB до пересечения с дугой ACB, называется высотой сегмента.
Сектор – эточасть круга,ограниченная дугой Am Bи двумя радиусами OAи OB, проведенными к концам этой дуги (рис.43).

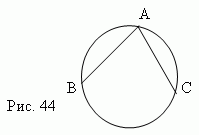
Углы в круге. Центральный угол – угол, образованный двумя радиусами ( AOB, рис.43). Вписанный угол – угол, образованный двумя хордами AB и AC, проведенными из их одной общей точки (BA C, рис.44). Описанный угол – угол, образованный двумя касательными AB и AC, проведенными из одной общей точки ( BAC, рис.41).
Длина дуги окружности пропорциональна её радиусу r и соответствующему центральному углу :
l = r
Таким образом, если мы знаем длину дуги
l и радиус r , то величина соответствующего центрального угла может быть определена их отношением: = l / r .Эта формула является основой для определения радианного измерения углов. Так, если l = r , то = 1, и мы говорим, что угол равен 1 радиану (это обозначается: = 1 рад ). Таким образом, мы имеем следующее определение радиана как единицы измерения углов: радиан – это центральный угол ( AOB, рис.43), у которого длина дуги равна её радиусу (Am B = AO , рис.43). Итак, радианная мера любого угла – это отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к её радиусу. В частности, в соответствии с формулой длины дуги, длина окружности C может быть выражена следующим образом:
где определяется как отношение C к диаметру круга 2 r :
= C / 2 r .
Иррациональное число; его приближённое значение 3.1415926…
С другой стороны, 2- это круговой угол окружности, который в градусной системе измерения равен 360º. На практике часто случается, что как радиус дуги, так и угол неизвестны. В этом случае длина дуги может быть вычислена по приближённой формуле Гюйгенса:
p 2l + (2l – L ) / 3 ,
где (см. рис.42): p – длина дуги ACB ; l – длина хорды AC ; L – длина хорды AB . Если дуга содержит не более чем 60 º , относительная погрешность этой формулы не превышает 0.5%.
Соотношения между элементами круга. Вписанный угол ( ABC , рис.45) равен половине центрального угла , опирающегося на ту же дугу AmC ( AOC , рис.45) . Поэтому, все вписанные углы (рис.45), опирающиеся на одну и ту же дугу ( Am C , рис.45), равны. А так как центральный угол содержит тоже количество градусов, чтои его дуга ( Am C ,рис.45), то любой вписанный угол измеряется половиной дуги, на которую он опирается (внашем случае Am C ).
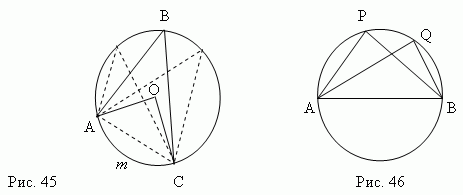
Все вписанные углы, опирающиеся на полукруг (APB, AQB, …, рис.46 ), прямые (Докажите это, пожалуйста!).
Угол (AOD, рис.47 ), образованный двумя хордами (ABи CD), измеряет ся полусуммой дуг, заключённых между его сторонами: (An D + Cm B) / 2 .

Угол (AOD, рис.48 ), образованный двумя секущими (AOи OD), измеряется полуразностью дуг, заключённых между его сторонами: (An D– Bm C ) / 2. секущей (COи BO), измеряется полуразностью дуг,заключённых между его сторонами: ( Bm C– Cn D ) / 2 .
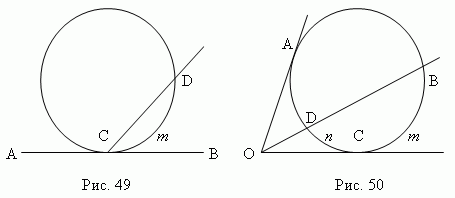
Описанный угол (AOC, рис.50 ), образованный двумя касательными (COи AO), измеряется полуразностью дуг,заключенных между его сторонами: ( ABC– CDA) / 2 .
Произведения отрезков хорд ( AB и CD , рис.51 или рис.52), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO .
К вадрат касательной равен произведению секущей на её внешнюю часть ( рис.50 ) : OA 2 = OB · O D (докажите!). Это свойство можно рассматривать как частный случай рис.52.

Хорда (AB, рис.53), перпендикулярная диаметру (CD), делится в их точке пересечения O пополам: AO = OB.
( Попробуйте доказать это! ).
Обладающих некоторым свойством.
1 / 3
✪ Определение параболы как ГМТ
✪ 124. Задачи на поверхности второго порядка. Геометрическое место точек
✪ Сопротивление материалов. Лекция 21 (тензор напряжений, главные напряжения)
Здравствуйте, дорогие друзья! Мы сейчас будем с вами заниматься геометрией, а потом алгеброй, а потом все смешаем и назовем это математикой. Очень простой вопрос. Представьте себе, что там, где я поставил белую точку, играет музыка (одна колонка). А потом появился техник и поставил колонку еще и на место розовой точки. Причем расстояние между ними довольно большое. Если вы встанете в зеленый крестик, то для вас музыка будет доноситься из двух мест с задержкой. Из одного с большей задержкой, чем из другого. Как бы встать так, чтобы слышать музыку левым и правым ухом совершенно одинаково, синхронно? То есть встать на равных расстояниях от двух колонок. Ответ очень простой, вы, конечно, знаете, если ходили хотя бы в 7 класс. А если не ходили, можете догадаться интуитивно. Надо построить отрезок, соединяющий розовую и белую точки, и в его центре (в его серединке) изобразить перпендикуляр. Тогда любая точка вертикального на этой доске перпендикуляра одинаково удалена от розовой и от белой. Почему так? Очень просто. Здесь два одинаковых треугольника. Почему они одинаковые? Потому что у них есть общая сторона, еще две стороны отмечены равными штрихами. И прямые углы тоже, конечно, равны друг другу. Как следствие, мы имеем право поставить равные отметки на таких сторонах. Итак, мы с вами нарисовали геометрическое место точек, одинаково удаленных от двух заданных точек. А как насчет двух прямых? Давайте нарисуем пару прямых. Я нарисую две параллельные прямые для начала. Это два берега и вы хотите плыть (по какой-то причине) на равных удалениях от этих двух берегов. Как построить эту траекторию? Давайте снова построим перпендикуляр к двум параллельным прямым. Найдем его середку. А дальше, вооружившись глазомером, пытаемся изобразить зеленую линию параллельно этим двум берегам. Конечно, если мы возьмем любую точку на этой зеленой линии и опустим перпендикуляр на какой-нибудь берег, то мы можем увидеть прямоугольник. А значит, эти стороны будут равны. Прямые могут и пересекаться. И тогда вы тоже легко решите такую задачу: множество точек, одинаково удаленных от этих двух прямых - это пара биссектрисс. Все эти решения строятся циркулем и линейкой и совершенно легко проходятся на геометрии. А сейчас я вам предложу еще одно множество, которое задается не двумя одинаковыми объектами, а один объект мы возьмем из первой задачи: где-то стоит точка, а другой объект - из второй: есть прямая. Причем эта точка нам нужна надолго, поэтому мы введем ей персональное имя: мы скажем, что это точка F. Прямая тоже персонализирована и называется буквой d. Представьте себе на мгновение, что это граница пляжа: выше пляж, а ниже море. А точка F - это, например, киоск с мороженым. И вы хотите сесть так, чтобы до киоска с мороженым и до берега было равное расстояние. Тогда пример такого места совершенно очевиден: точно так же, как и здесь, и здесь, мы строим перпендикуляр из точки F на прямую d, находим его середку и вот это самое выигрышное место: вам до киоска очень мало идти и до моря очень мало идти. А как по-другому можно сесть, чтобы тоже было одинаковое расстояние и до киоска, и до берега моря? Вот пример еще один. Если мы построим квадрат с такой стороной, то тогда равенство этих сторон и перпендикуляр здесь тоже нам гарантируют, что эта точка годится. Причем ясно, что раз пряж простирается в обе стороны, то и здесь мы можем нарисовать такой же квадрат. Решение будет симметрично. Давайте запишем решение для такой задачи. Мы ищем вот что: нам нужно множество букв М (точек, обозначенных буквой М), а условие на них вот какое: (вот эта годится быть буквой М) расстояние от любой точки из этого множества до F равняется... Вместо слова "расстояние" я сейчас напишу букву "ро", потому что я хочу расстояние от точки М до прямой d. Поскольку мы ищем множество, здесь стоят фигурные скобки. И мы ищем все такие точки, обозначенные буквой М, чтобы выполнялось это равенство. Две мы уже нашли. Я имею право обвести эту точку зеленым кружочком и эту тоже. Есть ли хотя бы одна точка между ними, которая принадлежит этому множеству? Одинаково удалена и от F, и от d. Да, есть. Давайте попробуем сделать следующее. Шагнем на какую-нибудь величину влево от известной нам точки из множества. Вопрос: тогда мы получим точку из этого же множества? Посмотрим на эту фигурку, на этот четырехугольник. Это прямоугольник, поэтому здесь тоже допустим один штрих. Расстояние от полученной точки до F как связано с этим отрезком? Конечно, оно больше, здесь нельзя поставить один штрих, потому что такой наклонный отрезок - это гипотинуза в треугольнике, где катет отмечен одним штрихом. Эта точка слишком низко, слишком близка к прямой d. Значит, надо ее немножко приподнять. Приподнять настолько, чтобы она достаточно удалилась от d и немножко приблизилась к F. Как именно - пока не будем выяснять, но это возможно. Идея такая: двигаясь влево и поднимаясь вверх, мы можем получать точки, принадлежащие множеству М. И если еще допустить, что шаг может быть сколь угодно маленьким, тогда поймем, что множество это непрерывно: это линия, которую можно нарисовать движением руки, не останавливаясь и нигде не перепрыгивая. И еще мы знаем, что линия симметрична. Эта зеленая линия является изображением этого множества, обозначенного фигурными скобками. Оказывается, это парабола. Это геометрическое определение для параболы. И здесь начинаются проблемы.
Роль дифференциалов во введении видовых различий в фигуру. Количество дифференциалов может быть любым; дифференциалов может и вовсе не быть.
Если заданы детерминант , где M {\displaystyle M} - точка, - дифференциалы, то искомую фигуру A {\displaystyle A} задают в виде: « A {\displaystyle A} - геометрическое место точек M {\displaystyle M} , таких, что P (M , a , b , c , …) {\displaystyle P(M,\;a,\;b,\;c,\;\ldots)} ». Далее обычно указывается роль дифференциалов, им даются названия применительно к данной конкретной фигуре. Под собственно фигурой понимают совокупность (множество) точек M {\displaystyle M} , для которых для каждого конкретного набора значений a , b , c , … {\displaystyle a,\;b,\;c,\;\ldots } высказывание P (M , a , b , c , …) {\displaystyle P(M,\;a,\;b,\;c,\;\ldots)} обращается в тождество. Каждый конкретный набор значений дифференциалов определяет отдельную фигуру, каждую из которых и всех их в совокупности именуют названием фигуры, которая задаётся через ГМТ.
В словесной формулировке предикативное высказывание озвучивают литературно, то есть с привлечением различного рода оборотов и т. д. с целью благозвучия. Иногда, в случае простых детерминантов, вообще обходятся без буквенных обозначений.
Пример : параболу зададим как множество всех таких точек M {\displaystyle M} , что расстояние от M {\displaystyle M} до точки F {\displaystyle F} равно расстоянию от M {\displaystyle M} до прямой l {\displaystyle l} . Тогда дифференциалы параболы - F {\displaystyle F} и l {\displaystyle l} ; детерминант - предикат P (M , F , l) = (ρ (M , F) = ρ l (M , l)) {\displaystyle P(M,\;F,\;l)=(\rho (M,\;F)=\rho _{l}(M,\;l))} , где ρ {\displaystyle \rho } - расстояние между двумя точками (метрика), ρ l {\displaystyle \rho _{l}} - расстояние от точки до прямой. И говорят: «Парабола - геометрическое место точек M {\displaystyle M} , равноудалённых от точки F {\displaystyle F} и прямой l {\displaystyle l} . Точку F {\displaystyle F} называют фокусом параболы, а прямую l {\displaystyle l} - директрисой».